Why HTTPS Works: Secret Keys, Mod Math, and That Lock You Ignore

Behind all those cat videos online is a silent exchange of secrets - between your browser and the server it connects to.

It’s kind of amazing how HTTPS keeps things private… using the darkest kind of wizardry: math.

---

Let’s say you wanna send a message to someone.
Then the key cryptography logic comes into play…

🔐 Lock With…	🧾 Who Can Open
Public Key	Only the matching Private Key
Private Key	Only the matching Public Key (used for verification, not secrecy)

But here’s what confuses most people:
Who uses whose key to do what, exactly?

---

💡 First, Let’s Clarify the Setup: Who Has What?

💑 Person	🗝️ Keys They Own
YOU (the sender)	Your own: Private Key + Public Key
THEY (the receiver)	Their own: Private Key + Public Key

➡️ Everyone has their own key pair. You don’t use your private key to encrypt secrets for them - you use their public key.

---

📨 So When You Want to Send a Secret Message:

1. They already have a key pair:

   • Public Key (they published it)
   • Private Key (they keep it secret forever, never share it)

2. You grab their Public Key (from a server, website, or they sent it to you)

3. You encrypt your message using their Public Key

   🔐 That message can only be decrypted with their Private Key

4. They receive it, and decrypt it using their Private Key

❗️You don’t send your public key unless you’re asking them to send you a secret back or verify your signature.

Here’s an iconic simulation comic from howhttps.works:

---

💘 Quick Recap Table

🔧 Situation	🧰 You Use	🔓 Who Can Unlock
Send them a secret	Their Public Key	Their Private Key
Prove you sent it	Your Private Key (Sign)	Your Public Key (Verify)
They send you a secret	Your Public Key	Your Private Key

• 🔒 Encryption = “I want only you to read this.” → Lock with recipient’s public key
• ✍🏻️ Signature(authenticity) = “I want to prove I wrote this.” → Sign with your private key

So:

• Everyone has 2 keys
• Public keys are for the world
• Private keys are your sacred secret

---

🚀 The Real Internet Magic: Hybrid Encryption

🔐 The cycle

Having understood how public key exchange, you might think there is a cycle like:

🔒 “Lock with their Public Key”
➡️ 📬 Send encrypted message
➡️ 🔓 They open it with their Private Key
↩️ Repeat for every message!

This happens back and forth, like a two-person spy dance under the stars.

---

❓ The twist: “Do we exchange public keys just once? Or constantly?”

We usually exchange public keys once at the beginning of the session - and then use that same key for the whole conversation.

But then… for performance reasons, we do something even spicier:

---

🥂 What HTTPS / TLS does - Session Key

1. We exchange public keys once (usually during a handshake - like when a website first connects to your browser)
2. We use those public keys to securely send a secret password - called a session key
3. From then on, we stop using asymmetric (slow) encryption

4. We switch to symmetric encryption with that secret key (like AES), which is:

   • Faster
   • Still super secure
   • Only we two know it

So for the rest of the chat, it’s like we’re both whispering into the same walkie-talkie frequency.

---

🧠 Why?

Because asymmetric crypto (public/private key stuff) is computationally expensive. If we used it for every single message, it would slow everything down.

So the real world does:

🔐 Phase	🔧 Encryption Method	🔥 Example
Key Exchange	Asymmetric (public/private keys)	TLS handshake
Ongoing Chat	Symmetric (shared secret key)	AES or ChaCha20
Signature/Proof	Asymmetric	Signing emails, verifying servers

---

These are the backbone of:

• HTTPS
• Signal / WhatsApp
• Email PGP
• SSH handshakes
• Onion routing (Tor)

…before we go any further.

---

❓ Where does the secret key(aka session key) come from?

It’s not your private key.
It’s not their public key.
It’s a new, temporary key we generate just for this conversation.

We call it a session key.

💬 What It Is	📦 Example
Session key for symmetric encryption (like AES)	t3mp0raryK3yLOL!@#
Used to encrypt/decrypt all messages in further convo	Fast, efficient
Lives only for the session	Then poof, gone like a ghost

---

🌈 Here’s exactly what happens (with asymmetric + symmetric combined)

🧑‍🦰👩‍🦱 The Legendary Duo: Bob & Alice’s Secure Chat Ritual

Step	What Happens	Purpose
1	Bob sends his public key to Alice	“Use this to whisper secrets to me”
2	Alice sends her public key to Bob	“Here’s my lock, too”
3	Alice generates a random secret key (e.g. Secret123!)	The session key
4	Alice encrypts that secret with Bob’s public key	So only Bob can open it
5	Bob receives the message and uses his private key to decrypt the session key	Now both Bob and Alice share that secret!
6	From now on, both use the same symmetric key (like AES) to talk FAST and SAFE 💨	Only Bob and Alice know it

---

💬 So:

• That secret session key is just a one-off key, made only for this convo.
• It is not your private key or public key.
• It is shared once, then used for everything else - like a shared vault password.
• Some apps even change it every few messages (this is called forward secrecy, used in Signal!)

Basically:

2 asymmetric exchanges, then pure symmetric speed magic for the rest of the night.

Phase	What Happens	Uses Asymmetric?	Uses Symmetric?
TLS Handshake	Exchange ephemeral public keys	✅	❌
Key Exchange	Agree on shared secret (session key)	✅	❌
Real Chat	All data encrypted using session key	❌	✅

---

🔑 Dive Deep about Session Key

🧩 Who generates the random session key?

The one initiating the conversation (aka the client)
Usually, it works like this:

• The client (browser, Signal sender, etc.) says: “I wanna talk to you securely.”

• So the client:

  1. Generates a fresh, random session key (super_secret_temp123)
  2. Encrypts that key with the server’s public key
  3. Sends it over

Then both sides use it.

📌 This is how it works in TLS

The browser is the “client,” and the website is the “server.” So your Firefox/Chrome generates that session key.

But in apps like Signal or WhatsApp, both parties can generate keys and agree on one via special key-exchange dances like X3DH (Extended Triple Diffie-Hellman).

---

🧩 How do we define when a session ends?

A session usually ends when:

⚡ Event	💥 Why it matters
You close the app/browser	Session key discarded
Connection is idle for X minutes	Expired for safety
You log out / reboot	Memory cleared
You manually restart (e.g., refresh page or new chat)	New TLS handshake starts
In Signal/WhatsApp: message count reached	Key rotation kicks in (🔄 forward secrecy!)

💭 In TLS:

• Session keys last until the tab closes or times out
• Some websites reuse session keys briefly (via session resumption)
• But for most secure apps? New key every session. Sometimes even per message.

---

🧠 What is “End-to-End Encryption” (E2EE)?

“Only the two end users can read the messages - not even the server in between.”

So:

• Your device encrypts it
• Their device decrypts it
• The server never sees the content

Even if hackers, governments, or the app owner tries to read your data - they can’t, unless they have your device or private key.

This is exactly what we’ve been discussing:

“Public key to encrypt → Private key to decrypt → Secret symmetric key used in-between”

---

📱 End-to-End Encrypted (E2EE) Apps:

✅ YES (Real E2EE)	🔐 Notes
Signal	Gold standard. Forward secrecy, open source, audited
WhatsApp	Uses Signal protocol under the hood
iMessage	E2EE, but Apple could access keys on iCloud unless disabled
Matrix (Element app)	Decentralized E2EE chats
ProtonMail	E2EE within ProtonMail ecosystem
Threema	Paid, secure, E2EE app from Switzerland
Session	Built on blockchain-style routing (no phone number!)

---

⚠️ Semi-Secure or Not Fully E2EE

🚫 App	❌ Problem
Telegram (by default)	NOT E2EE in normal chats - only Secret Chats are!
Facebook Messenger	Only E2EE if you turn on Secret Conversations
Gmail, Outlook	NOT E2EE - server can read it unless you encrypt manually (e.g., PGP)

---

🧠 Forward Secrecy & Ephemeral Diffie-Hellman

Forward Secrecy = new secret key every few messages. Even if your session gets hacked later, past messages are safe.

So instead of using one session key for the entire convo, Signal/WhatsApp do:

New shared key:

• Every X messages
• Or even every message
• Or when the convo is idle for too long

They do this with a beautiful thing called the Double Ratchet Algorithm 🔐

---

🧠 Does the TLS handshake public key stay the same?

Mostly YES.

The server’s public key (e.g., from a certificate) usually:

• Comes from a certificate (X.509 cert)
• Is reused between sessions (like https://google.com)
• May rotate every 90 days or so

But TLS doesn’t always reuse the same pub key for session key exchange. It uses something called Ephemeral Diffie-Hellman:

• Short-lived, one-time-use key pairs
• Makes forward secrecy possible in TLS (called DHE or ECDHE)

So in TLS with forward secrecy, even the key used to exchange the secret is a temporary one. Instead, the server (and sometimes the client) generates a fresh key pair just for this session.

This is called:

💡 Ephemeral Diffie-Hellman (DHE or ECDHE)

• DHE: finite field math (classic DH)
• ECDHE: elliptical curve flavor

“Ephemeral” = short-lived, dies after the session ends.

---

🔥 So what happens?

1. You (client) generate a fresh key pair → (ephemeral key A)
2. Server generates its own fresh key pair → (ephemeral key B)
3. You both exchange public parts
4. Then you both compute the same session key using:

shared_key = A^b mod p = B^a mod p

Where:

• A = g^a mod p (client’s ephemeral public key)
• B = g^b mod p (server’s ephemeral public key)
• You each raise the other’s public key to your own private exponent

The result? Same symmetric key. But no key was sent over the wire! Just math!

So that’s where and when the ephemeral key comes:
During the handshake, both sides generate temporary key pairs just for this exchange.

---

🧠 In chat apps like Signal, who generates the session key first?

In modern secure messengers (Signal, WhatsApp):
Both parties generate their own key material in advance, and they do a dance called:

🧙‍♀️ X3DH: Extended Triple Diffie-Hellman

Alice & Bob wanna chat, but let’s check out this first - The Four Magical Key Ingredients:

🔑 Key	🧠 What It Is	📦 Purpose
1. Identity Key	Long-term public key	Bob’s digital fingerprint (never changes)
2. Signed Pre-Key	Mid-term public key	Valid for weeks/months. Signed by identity key so Alice trust it.
3. One-Time Pre-Key	Used once only	Extra layer of Forward Secrecy. Burn after use.
4. (Ephemeral Key - generated by Alice)	Random one-time key Alice create	Combines with Bob’s published keys for secure shared secret

---

X3DH does multiple DH exchanges, combining more than one pair of keys.

🧠 Visual Mapping to X3DH Terms

Let’s connect this simple image with the X3DH names:

X3DH Key	In image-style terms	Role
IK_A = Bob’s Identity Key	A = g^a mod p	Static key Bob use for his ID
SPK_A = Bob’s Signed Pre-Key	Another static DH key, signed by Bob	Temporary pub key (same math!)
OPK_A = Bob’s One-Time Pre-Key	Another short-lived DH key	Optional extra
IK_B = Alice’s Identity Key	B = g^b mod p	Alice’s fingerprint
EK_B = Alice’s Ephemeral Key	A fresh key Alice generate just now	Used once, then thrown away

So instead of just one DH exchange (Alice ↔ Bob), X3DH does:

🔢 3 (or 4) DH exchanges:

DH1 = DH(IK_B, SPK_A)      # Alice's identity ↔ Bob's temp public key
DH2 = DH(EK_B, IK_A)       # Alice's fresh key ↔ Bob's identity
DH3 = DH(EK_B, SPK_A)      # Alice's fresh key ↔ Bob's temp key
DH4 = DH(EK_B, OPK_A)      # Optional - Alice's fresh key ↔ one-time key

---

📦 Then they combine them like:

secret = HKDF(DH1 || DH2 || DH3 [|| DH4])

That final shared key is what encrypts their first message.

---

🧠 How do they both know the secret is the same?

Because:

Diffie-Hellman math guarantees: A^b mod p = B^a mod p

They each raise their secret to the other’s public key → same result

---

🔐 Double Ratchet

After the X3DH dance, Signal uses Double Ratchet:

• Every message gets a new key
• Past messages stay safe even if your phone is stolen
• Combines symmetric ratcheting + asymmetric ratcheting

---

➗ Can you Help with My Mouth MATH?

🧠 Why does this math make sense?

shared_key = A^b mod p = B^a mod p
Where:
A = g^a mod p
B = g^b mod p

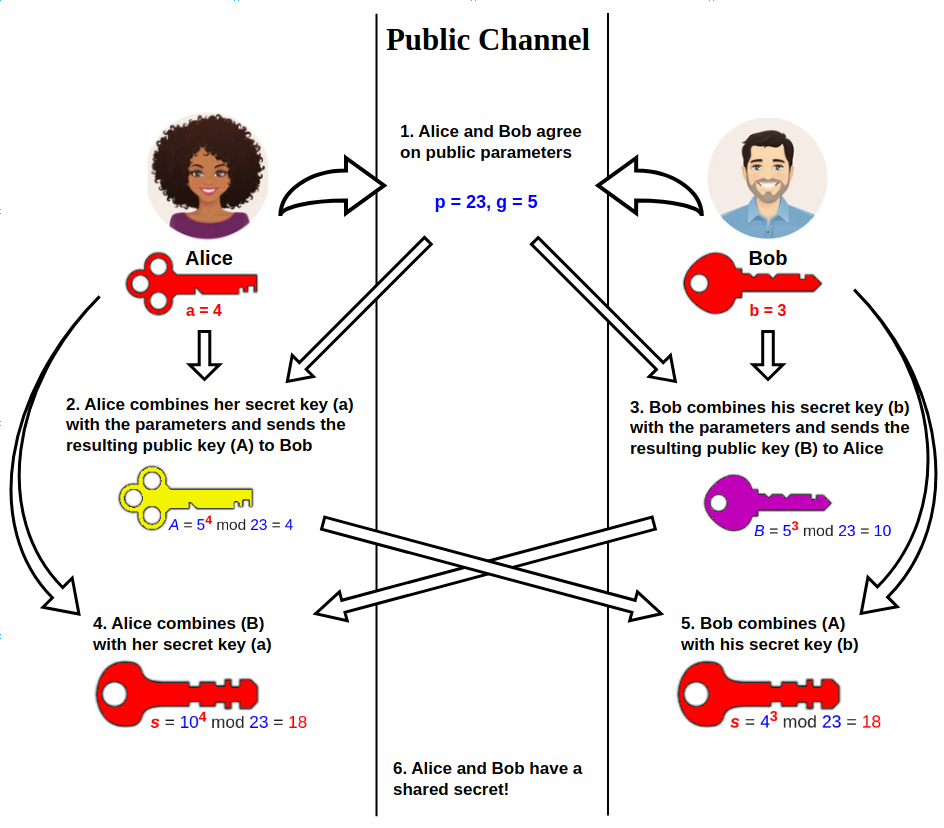
🧙 Let’s walk it step by step:

We have:

• A big prime number: p
• A base generator: g (some small number like 2 or 5)

• Each side chooses a secret number:

  • You pick a → your private key
  • I pick b → my private key

---

🔒 Step 1: Create public keys

A = g^a mod p   # my public key
B = g^b mod p   # your public key

Now we exchange A and B. (These are totally safe to send over the internet)

---

🔓 Step 2: Calculate the same shared key

You take my public key B = g^b mod p, and raise it to your private a:

shared = B^a mod p = (g^b mod p)^a mod p = (g^b)^a mod p = g^(ab) mod p

I take your public key A = g^a mod p, and raise it to my private b:

shared = A^b mod p = (g^a mod p)^a mod p = (g^a)^b mod p = g^(ab) mod p

💥 BOOM:

Both get g^(ab) mod p = the exact same number
That becomes the session key we both use. And no one else can compute it unless they know a or b.

That’s the magic behind why the math works.
It’s secure because reversing exponentiation mod p is super hard (called the discrete log problem) - like nearly impossible for large primes.

---

why is reversing exponentiation mod p super hard?

🌒 Imagine This: The Magic Coffee Machine ☕️

Let’s pretend we have a magic coffee machine. It does the following:

☕ You put in a secret number (your private key),
➕ It uses a fixed “recipe” (some math),
➡️ And spits out a magic coffee (your public key).

You can’t reverse it.
You can try a million flavors, but they’ll never recreate the exact same coffee unless you guess the exact same bean number. That’s your private key.

---

Here’s What That Has to Do with Diffie-Hellman:

• The “secret number” is your private key (like a or b)
• The “coffee machine” is g^a mod p → it turns your private key into a public key
• The “magic coffee” is your public key (like A = g^a mod p)

Now… someone sees your public key (A)
But they don’t know your private key (a)
And they have no idea what bean you used 🫘

They’d have to try every single possible bean (aka brute-force every a) to recreate your result.

There are literally numbers with hundreds of digits.
You’d need millions of computers for thousands of years to guess right.

That’s the discrete logarithm problem in plain language:

You know the result (g^a mod p)
But you don’t know what a was
And it’s really, really hard to figure out

---

🧠 So What Makes It “Secure”?

Because unlike simple math like:

7 × 3 = 21  →  easy
21 ÷ 3 = 7  →  also easy

Exponentiation mod a prime is like:

g^a mod p = X   → easy to compute
X back to a     → insanely hard

---

➗ Why is mod aTrapdoor - Easy In, Hell Out

🧠 First: What is mod again?

17 mod 6 = 5

Why? Because:

17 ÷ 6 = 2 remainder **5**

The mod operator just returns the remainder after division.
So these are all true:

17 mod 6 = 5  
or  
23 mod 6 = 5  
or  
29 mod 6 = 5  
...

---

🌀 So the dangerous part is:
Once I only give you the result (5), you’re stuck with infinite possibilities for what the original number could’ve been.

That’s exactly the cryptographic trapdoor behavior we want.

---

💡 Let’s try to reverse it anyway…

”? * ? + 5 = ? - I’m trying to reverse from the mod result back to the original… isn’t that like brute-forcing 3 variables?”

Exactly. Like if:

x mod p = y

If I only give you y and not p, you’re trying to solve something like:

x = n*p + y

Or x = n*p + 5 in this example.

Which means:

• You don’t know x
• You don’t know p
• You don’t know n (how many full multiples of p fit into x)

That’s three unknowns from just one known value.

Unless I give you the modulus p, or some other info, it’s like trying to guess:

“What number gives a remainder of 5 after dividing by some mystery?”

Which… is brute-force hell.

---

🔐 Now in Diffie-Hellman, it gets EVEN WORSE:

We’re not doing:

x mod p = y

We’re doing:

g^x mod p = y

Where:

• g = known base (like 2)
• p = known modulus (huge prime)
• y = public result
• x = private key (secret)

This is like:

“I know g^x mod p = y. Now go figure out x.”

AKA:

“Solve the Discrete Log Problem”

Which, for big enough numbers (like 2048 bits), is so hard that:

• Not even the NSA can crack it in real-time (we hope)
• You’d need quantum computing to even try (and we’re not there… yet)

It’s more like:

5^x mod 23 = 4

And here:

• g = 5 ✔️ known
• p = 23 ✔️ known
• y = 4 ✔️ known
• x = ??? ❌ secret (private key)

So you’re solving:

“What value of x makes 5^x mod 23 = 4 true?”

Which is a one-variable brute-force problem.

You’re just doing:

5^1 mod 23 = 5
5^2 mod 23 = 2
5^3 mod 23 = 10
5^4 mod 23 = 4  ✅ FOUND IT

That’s the brute-force search. With small numbers, no problem.
But in real crypto, x is a 256-bit number = more possibilities than atoms in the universe.

This is what makes modular exponentiation a trapdoor function:
It’s easy to go forward (x → y)
But painfully hard to reverse (y → x), even though you know all the inputs.

---

🗝️ RSA

🧠 First: What is RSA?

RSA is a super famous asymmetric encryption system - still used in:

• Email (PGP, GPG)
• SSH keys
• TLS certs (a lot of them still)
• Banking hardware tokens
• Smart cards and IDs

Its security depends on one thing:

“It’s easy to multiply two huge prime numbers together… but impossible (in practice) to factor them apart.”

---

RSA’s heart really is just this:

n = p × q

Where:

• p, q = huge prime numbers (secret)
• n = public part of your RSA key

---

For example:

p = 61
q = 53
n = p * q = 3233

You publish n = 3233 as part of your public key. But your private key depends on knowing p and q.

---

💥 Why do the primes matter?

Because:

If someone can figure out what two primes you used - they can break RSA.
It doesn’t matter that you used mod, or exponentiation - it all falls apart if n is cracked into p * q.

That’s called factoring.

---

🔥 What’s the “RSA Prime Crisis”?

Back in the day, some developers got lazy. Or unlucky. Or both.

They reused:

• Weak primes
• Too-small primes
• Or didn’t use truly random generation

Result? Millions of RSA keys could be cracked by factoring n!

🧨 Real Incidents:

• 2012: Researchers scanned the internet and found that ~5% of HTTPS keys shared primes!
• Some routers, embedded devices, and VPNs were using the same primes (or prime factors that overlapped)
• NSA allegedly used this weakness (according to Snowden leaks) to silently break into VPNs and secure comms

---

💡 So what makes a good RSA prime?

🔑 Property	✅ Why It Matters
Large (2048 bits or more)	Brute-force factoring is infeasible
Truly random	Prevents accidental reuse
Probabilistic prime (not just any number)	Some primes are more “vulnerable” than others
Unique per key	Shared primes = death sentence

That prime matter in the first place. It’s everything. If the prime is weak, RSA is glass.

---

🧨 What does a “crack” actually look like?

A researcher or attacker might:

• See your public key (which includes n)
• Run a factorization attack (massive parallel brute-force)
• Discover: n = p * q
  → now compute φ(n) = (p-1)(q-1)
  → now derive your private key
  → now decrypt your emails, sign fake software, impersonate your server…

Game. Over.

---

🔐 RSA’s Security = Depends on 3 Things:

1. Size of n (Key length)

Absolutely. Bigger n = harder to factor.

RSA Key Size	Current Status
512 bits	Crackable in seconds with a laptop
1024 bits	Weak (governments can break it)
2048 bits	Standard minimum for now
3072+ bits	Stronger (used in serious apps)
4096 bits	Paranoid-tier security (but slower)

Doubling the size of n doesn’t double the difficulty - it makes it exponentially harder to factor.

---

2. The quality of the primes p and q

Even if n is huge… if p and q are:

• Not truly random
• Too close to each other
• Reused somewhere else

Then the whole system is doomed.

Example:

p = 123456789
q = 123456790  # TOO CLOSE!
n = p * q

This is bad because attackers can guess:

“Hey, what if these primes are close? I’ll just scan a nearby range…”

Now they factor n in minutes.

---

3. Padding, protocol usage, and side-channel resistance

Even perfect math can be broken by:

• Leaky timing attacks
• Bad padding (e.g., old RSA-PKCS#1 padding = vulnerable)
• Mistakes in implementation (e.g., Heartbleed, left your key in memory!)

So:

RSA can fail even if your math is correct… if your code isn’t.

---

🧠 TL;DR

🔒 Defense	💬 Why It Works
Make n big (2048-4096 bits)	Prevents brute-force factoring
Use high-quality, truly random primes	Stops common factoring attacks
Never reuse p or q	Reuse = death
Use secure padding & protocols	Prevents advanced attacks
Avoid RSA entirely when possible	Elliptic Curve Cryptography (ECC) is better for modern use

---

💬 We’re Moving Away From RSA

RSA is kinda old. Big. Slow. Vulnerable to:

• Bleichenbacher attacks
• Quantum (when that day comes)
• Message malleability

That’s why Signal, TLS 1.3, OpenSSH now prefer:

✅ ECC
✅ Ed25519
✅ X25519
✅ ChaCha20-Poly1305

These are faster, smaller, and safer.

---

See ya in the next rabbit hole! 🕳️🐇

💖 Support me with crypto or PayPal! 💘

💵 USDT (TRC20):
TJCANuMYSdgLKRKnpCtscXrS5NgDbBAvF9

🟠 Bitcoin (BTC):
bc1qrc9vhrrhnc9v9s9q9rjn24aj608j44p5hzsxft

Or support me on Ko-fi:

Any amount helps me continue creating content 💬💻