🏫 [CS50x 2025] 5 Data Structures

🔗 Linked Lists

To implement a sorted linked list of numbers, we have:

int main(void)
{
    // Memory for numbers
    node *list = NULL;

    // Build list
    for (int i = 0; i < 3; i++)
    {
        // Allocate node for number
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = get_int("Number: ");
        n->next = NULL;

        // If list is empty
        if (list == NULL)
        {
            list = n;
        }

        // If number belongs at beginning of list
        else if (n->number < list->number)
        {
            n->next = list;
            list = n; 
        }

        // If number belongs later in list
        else
        {
            // Iterate over nodes in list
            for (node *ptr = list; ptr != NULL; ptr = ptr->next)
            {
                // If at end of list
                if (ptr->next == NULL)
                {
                    // Append node
                    ptr->next = n;
                    break;
                }

                // If in middle of list
                if (n->number < ptr->next->number)
                {
                    n->next = ptr->next;
                    ptr->next = n;
                    break;
                }
            }
        }
    }

    // Print numbers
    ...

    // Free memory
    ...
}

This chunk is probably the trickiest.

if (n->number < ptr->next->number)
{
    n->next = ptr->next;
    ptr->next = n;
    break;
}

---

🎯 Let’s visualize it

Let’s say your list currently looks like this:

[2] → [5] → [8] → [10]

And the new number is 6.

We want to insert 6 in the right place so the list stays sorted.

Now we walk with a pointer (ptr) starting at the head:

• ptr points at [2], ptr->next is [5] - 6 < 5? ❌
• ptr moves to [5], ptr->next is [8] - 6 < 8? ✅

BOOM. This is where we need to insert 6!

---

🔧 So what does the code do?

n->next = ptr->next;

• New node (n) is pointing to what ptr was previously pointing to (e.g. [8]).

ptr->next = n;

• Now the current node’s next is the new node!

So it becomes:

[2] → [5] → [6] → [8] → [10]

A perfect little insertion.

---

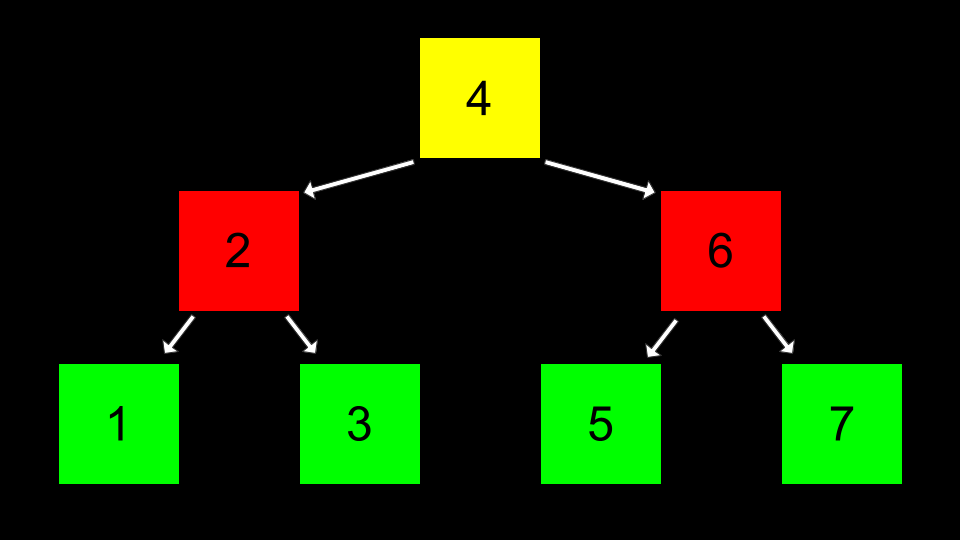
🌲 Trees

To make this 3 generations tree into code,

we have:

// Implements a list of numbers as a binary search tree

#include <stdio.h>
#include <stdlib.h>

// Represents a node
typedef struct node
{
    int number;
    struct node *left;
    struct node *right;
}
node;

void free_tree(node *root);
void print_tree(node *root);

int main(void)
{
    // Tree of size 0
    node *tree = NULL;

    // Add number to list
    node *n = malloc(sizeof(node));
    if (n == NULL)
    {
        return 1;
    }
    n->number = 2;
    n->left = NULL;
    n->right = NULL;
    tree = n;

    // Add number to list
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        free_tree(tree);
        return 1;
    }
    n->number = 1;
    n->left = NULL;
    n->right = NULL;
    tree->left = n;

    // Add number to list
    n = malloc(sizeof(node));
    if (n == NULL)
    {
        free_tree(tree);
        return 1;
    }
    n->number = 3;
    n->left = NULL;
    n->right = NULL;
    tree->right = n;

    // Print tree
    print_tree(tree);

    // Free tree
    free_tree(tree);
    return 0;
}

void free_tree(node *root)
{
    if (root == NULL)
    {
        return;
    }
    free_tree(root->left);
    free_tree(root->right);
    free(root);
}

void print_tree(node *root)
{
    if (root == NULL)
    {
        return;
    }
    print_tree(root->left);
    printf("%i\n", root->number);
    print_tree(root->right);
}

---

🌳 Understand tree = n;

tree = n;

We earlier had this:

node *tree = NULL;

Which means:

“I’m declaring a pointer called tree that will eventually point to the root of the binary tree.”

Then created the first node (with number 2), like this:

node *n = malloc(sizeof(node));
n->number = 2;
n->left = NULL;
n->right = NULL;

Now this new node n exists in memory - it’s the root of your future tree.

So when we do:

tree = n;

We’re saying:

“Let tree point to the root node (which we just created and stored in n).”

---

🫆 Print Recursion

void print_tree(node *root)
{
    if (root == NULL)
    {
        return;
    }
    print_tree(root->left);
    printf("%i\n", root->number);
    print_tree(root->right);
    // no need this line 👇🏻
    // print_tree(root->right);
}

This is called: in-order traversal.

Left → Root → Right

So if your tree looks like:

    2
   / \
  1   3

The steps are:

1. Go to left subtree → print 1
2. Print 2
3. Go to right subtree → print 3

This gives:

1
2
3

When we call:

print_tree(tree);  // tree points to root = 2

---

🔁 Recursion Steps (visually)

print_tree(2)
├── print_tree(1)
│   ├── print_tree(NULL) → returns
│   ├── print 1
│   └── print_tree(NULL) → returns
├── print 2
└── print_tree(3)
    ├── print_tree(NULL) → returns
    ├── print 3
    └── print_tree(NULL) → returns

---

🧾 Printed Output:

1
2
3

That’s recursion: the function calls itself, each time focusing on a smaller part of the tree. Once it hits NULL, it climbs back up the call stack and finishes printing the current node, then goes to the right.

---

🧪 random() % 2

It says: “Give me a random number, but I only care whether it’s 0 or 1.”

Because:

random() → gives you a **big random integer** (like 7834724 or 902394)
% 2      → turns it into either 0 or 1

🎲 This is like flipping a coin

random() value	random() % 2 result
4582738	0
9204737	1
8273418	0
…	1 or 0 randomly

---

🤔 Why does it feel weird & What does random() % 2 actually do?

“Give a big random number… and then just mod 2 it into 0 or 1? Why not directly get 0 or 1?”

That’s the illusion of complexity:

• We’re using a full-sized random number generator to simulate something super small (a coin flip).
• It feels wasteful, and it kinda is - but it works fine.

random() % 2:

• Calls a system-level random number generator (which gives a big number, maybe 32-bit or 64-bit).
• Then throws away most of that randomness by doing % 2, just keeping the least significant bit (either 0 or 1).

---

🔎 A better method - random() & 1

int random_bit()
{
    return random() & 1; // faster, just grabs the lowest bit
}

This is bitwise AND, not regular math.

random() & 1

means:

Take the random number, and keep only its least significant bit (the very last bit, the “1s place”).

---

✔️ How it works

First, what is & ?

It’s called the bitwise AND operator. It compares each bit in two numbers:

Rule:

1 & 1 = 1
everything else is 0:

• 1 & 0 = 0
• 0 & 1 = 0
• 0 & 0 = 0

---

Now let’s say random() gives you this 8-bit number (pretend for simplicity):

random() = 01101110  (binary) = 110 in decimal

Now do:

01101110   (random number)
& 00000001   (binary for 1)
----------
00000000   → means even → result is 0

Another example:

   1 0 1 1 0 1 1 1   (random number in binary)
&  0 0 0 0 0 0 0 1   (only the last bit is 1)
-------------------
   0 0 0 0 0 0 0 1   → Result: 00000001 (which is just `1`)

So essentially:

• If the last bit is 0 → result is 0 (even number)
• If the last bit is 1 → result is 1 (odd number)

Everything else gets wiped out.

That’s a fast way to flip a coin:

• 0 = heads
• 1 = tails

---

🕒 srandom(time(0));

It’s doing two things:

1. time(0)

   This returns the current time in seconds since January 1, 1970 (Unix Epoch). So every time you run your program, this number changes - unless you run it again in the same second.

   Example:

    time(0)  →  1718501826   // A big changing number, like a timestamp
   

2. srandom(...)

   This is like “planting a seed” into your random number generator. It tells the system:

   “Hey, start the randomness with THIS specific number.”

   So:

    srandom(time(0));
   

   is basically:

   “Use the current time as the seed to start randomness!”

   Because if you don’t do this, then your program will give the same “random” numbers every time you run it.

---

💡 Since time(0) changes every second, why not just use it directly?

time(0) is just a number

If you write:

int r = time(0) % 2;

You’re not getting randomness - you’re just splitting the current second into either 0 or 1. So the result only changes once per second, and it’s 100% predictable.

Imagine:

time(0) = 1718502033   → 1718502033 % 2 = 1
time(0) = 1718502034   → 1718502034 % 2 = 0

That’s not “random” - that’s a clock. Not chaos.

But with srandom(time(0)), we’re doing this:

// Set the seed
srandom(time(0)); // 🌱

int a = random(); // 🎲 fully chaotic
int b = random(); // 🎲 new chaos from same seed

This way, you initialize the random number generator using the current time - so:

• Each time you run the program in a new second, it uses a different seed, and therefore gives totally different random numbers.
• But within the same run, it produces a whole sequence of chaotic values.

---

📊 Example

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main(void)
{
    srandom(time(0)); // 🧪 seed it with current time

    // Print 5 random numbers
    for (int i = 0; i < 5; i++)
    {
        printf("Random %d: %ld\n", i, random());
    }

    return 0;
}

Run this once:

Random 0: 123456789
Random 1: 219838201
Random 2: 882182838
Random 3: 498192388
Random 4: 388128127

Wait 2 seconds…

Run again:

Random 0: 129192139
Random 1: 473882019
Random 2: 892831002
Random 3: 192139103
Random 4: 182391281

Different every time.